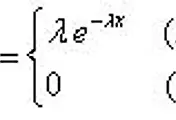Poisson Distribution 포아송 분포
1. 포아송 분포 (Poisson Distribution)
ㅇ 근대확률론의 기초를 확립한 사람중의 한사람인 수학자 포아송(1781~1840)이 제시한
확률적 특성을 따르는 확률분포
ㅇ 한정된 특정 시간 또는 공간 내에서 사건 발생 수가 따르는 확률분포
- 주로 시간적이나 공간적으로 발생빈도가 낮은 희귀한 사건의 수 등이 잘 설명됨
2. 포아송 분포 특징
ㅇ 표기 : X ~ Poi(λ)
- 모수 λ인 포아송 분포
ㅇ 확률질량함수

- x는 0,1,2,3, ...등 사건 발생 수
- λ는 일정 단위 시간 또는 공간 당 평균적으로 발생하는 사건 횟수
ㅇ 기대값

ㅇ 분산

ㅇ 포아송 분포는 이항분포(Binomial Distribution)의 특수한 경우(극한 분포)로 유도
될 수 있음.
- 즉, 이항분포가 성공률이 작고 시행횟수가 클 경우에 포아송 분포에 근사하게 됨
3. 포아송 분포 전제조건
ㅇ 독립성
- 단위 시간이나 공간에서 발생하는 사상은 서로 통계적 독립
ㅇ 일정성
- 단위 시간이나 공간에서 발생확률은 동일
ㅇ 비집락성
- 2 이상의 사상이 극히 작은 공간에서 발생할 확률은 무시할 정도로 작음
※ 즉, 사건 발생이 서로 통계적 독립이고, 사건 발생 확률이 일정하며, 아주 작은 단위
의 시간(공간)에서의 사건 발생 확률은 0 임.
4. 포아송 분포 응용
* 한정된 시간 및 공간에서 사건 발생 확률을 구하는데 유용
- 시간당 손님의 방문 수라든지, 월간 기계의 고장 횟수, 단위길이당 균열의 발생 수
등과 같이 지정된 시간 또는 장소 등에서 어떤 사건이 발생할 확률을 예측
ㅇ 포아송 분포 응용 例
- 단위시간당 교차로를 지나가는 자동차 대수
- 단위면적당 결점의 수
- 어떤 책의 임의 페이지에서 잘못 인쇄된 글자의 수
- 하루 동안 잘못 걸린 전화의 수
- 주어진 하루 동안 방문한 고객의 수
- 통신에서의 트래픽 등이 포아송 분포를 따르고 있다고 알려짐
. 트래픽량을 발생호수에 따라 실측표시하여 보면 그 분포가 근사적으로 포아송 분포
를 따르고 있음을 알 수 있음
'BigData > 수학이론' 카테고리의 다른 글
| 확률분포 > 지수분포 (0) | 2015.03.17 |
|---|---|
| 확률분포 > 균등분포 (0) | 2015.03.17 |
| 확률분포 > 정규분포 (0) | 2015.03.17 |
| 거리(distance) 구하기 (0) | 2015.03.16 |